○16進数で大きな桁数の計算を行う
■はじめに
プログラムでは変数によって表現できる値の最大値がきまってますよね
1バイトだと256ですし、2バイトだと65536ですし、
もっともっと大きい数を計算したい時どうすればいいんでしょうか？
えっ？64bit変数とか使えばいいって？
もっともっと大きな数なら、浮動少数点型とか使えば解決するって？
いやいや、64bit変数では0x0000000000000000から0xFFFFFFFFFFFFFFFFまでしか
表現できませんし、浮動小数点型では正確な値を保持できません
(浮動小数点型の誤差を見たいのなら0.1をループで1000回ぐらい加算して
結果を表示させてみてください)
たとえば、数百桁の計算をしなければいけない時とか、どのようにすれば計算
出来るのか？
今回はそれを考えて見たいと思います
■加算について考える
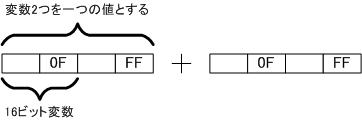
大きな数を表現するために複数の16ビット変数(配列)をまとめて一つの変数としたいと思います
0x0FFFを変数に格納するにあたって0Fを前の変数に代入して、FFを後ろの変数に代入し
1バイト単位で区切って、値を表現したいと思います
0x0FFF + 0x0FFF を表現すると次のようになります
▼計算を行う
①まず最初に桁の下位側の変数の1バイト分の加算を行い、結果(2バイト)を変数に格納します
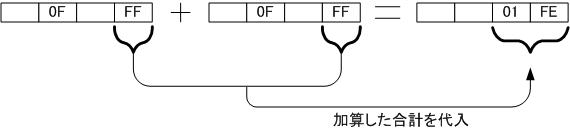②次の上位桁の変数の加算を行う時は、上位桁の変数同士を加算して、そこに、
下位の桁の計算結果の上位8ビットを加えます。
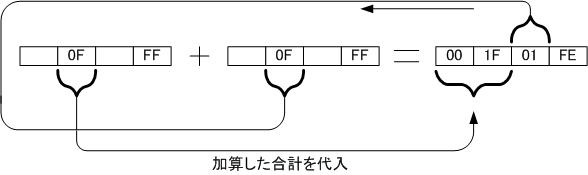③計算結果の上位ビットをマスクして計算結果とします
▼上記計算方法で複数の変数にわたる値の加算が出来るはずです
簡単なテストプログラムを作成して確認してみます
#include <stdio.h>
int main(){
unsigned short a[2],b[2],c[2];
a[1]=0x0F;
a[0]=0xFF;
b[1]=0x0F;
b[0]=0xFF;
c[0]=a[0]+b[0];
c[1]=a[1]+b[1]+(c[0]>>8);
printf("%02x %02x\n",(unsigned char)c[1],(unsigned char)(c[0] & 0xFF));
return 0;
}
プログラムを実行
c:\>■■■.exe
1f fe
関数電卓を使って確認すると、
0x0FFF + 0x0FFF = 0x1FFE
電卓の計算結果と同一です
加算方法が正しいことが確認できました
▼プログラム作成
テストプログラムが正しく動作しましたので、それを修正して
配列を一つの変数として加算できるようにしたいと思います
配列サイズはとりあえず4としますが、もっと大きい数にすれば大きな桁数も計算できます
#include <stdio.h>
void add(unsigned short*a,unsigned short*b,unsigned short*c,int size){
c[0]=(a[0] & 0xFF)+(b[0] & 0xFF);
for(int i=1;i<size;i++){
c[i]=(a[i] & 0xFF)+(b[i] & 0xFF)+(c[i-1]>>8);
}
}
int main(){
unsigned short a[4],b[4],c[4];
a[3]=0x12;a[2]=0x34;a[1]=0x56;a[0]=0x78;
b[3]=0x9A;b[2]=0xBC;b[1]=0xDE;b[0]=0xF0;
add(a,b,c,(sizeof(a)/sizeof(a[0])));
for(int i=(sizeof(a)/sizeof(a[0]))-1;i>=0;i--){
printf("%02x ",(unsigned char)(c[i] & 0xFF));
}
printf("\n");
return 0;
}
プログラムを実行
c:\>■■■.exe
ac f1 35 68
上記プログラムは 0x12345678 + 0x9ABCDEF0 を行っていますので
関数電卓で確認すると
0x12345678 + 0x9ABCDEF0 = 0xACF13568
計算結果が同一ですのでプログラムが正しく動作していることが確認できます
■減算について考える
加算が出来ましたので次は減算を行いたいと思います
減算の考え方として
10 - 1 = 9
上記式は考え方を変えると
10 + (-1) = 9
として表現することが出来ます
つまり、引き算は足し算で行うことが出来るということを意味します
そこで、1 を -1 に変換する方法とは
ビットを反転して1を足す(２の補数)とマイナス値にすることができます
10進数の 1 を2進数で表現 → 0000 0001 →ビットを反転→ 1111 1110 → 1を足す →
→ 1111 1111 →10進数に戻す→ -1
マイナス値に変換して加算する事により引き算を行ってみます
▼加算プログラムを修正して減算も出来るように変更
#include <stdio.h>
void add(unsigned short*a,unsigned short*b,unsigned short*c,int size){
c[0]=(a[0] & 0xFF)+(b[0] & 0xFF);
for(int i=1;i<size;i++){
c[i]=(a[i] & 0xFF)+(b[i] & 0xFF)+(c[i-1]>>8);
}
}
void sub(unsigned short*a,unsigned short*b,unsigned short*c,int size){
c[0]=((~b[0]) & 0xFF)+0x01;
for(int i=1;i<size;i++){
c[i]=((~b[i]) & 0xFF)+(c[i-1]>>8);
}
add(a,c,c,size);
}
int main(){
unsigned short a[4],b[4],c[4];
a[3]=0xFF;a[2]=0xFF;a[1]=0xFF;a[0]=0xFF;
b[3]=0x12;b[2]=0x34;b[1]=0x56;b[0]=0x78;
sub(a,b,c,(sizeof(a)/sizeof(a[0])));
for(int i=(sizeof(a)/sizeof(a[0]))-1;i>=0;i--){
printf("%02x ",(unsigned char)(c[i] & 0xFF));
}
printf("\n");
return 0;
}
プログラムを実行
c:\>■■■.exe
ed cb a9 87
上記プログラムは 0xFFFFFFFF - 0x12345678 を行っていますので
関数電卓で確認すると
0xFFFFFFFF - 0x12345678 = 0xEDCBA987
電卓の計算結果と同一です
減算方法が正しいことが確認できました
■掛け算について考える
掛け算の考え方として、掛ける数の回数だけ繰り返し足し算を行えば
計算できます。
しかし、それでは効率が悪いため、計算機の中では次のように処理されます
内容的には繰り返し足し算していると同じ意味です
▼ステップ 1
2進数表記で1010と0011を掛け算します
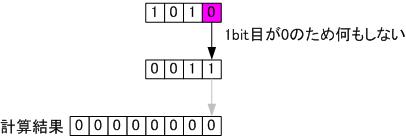▼ステップ 2
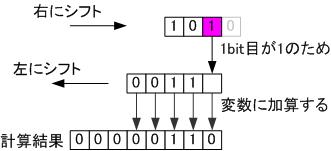▼ステップ 3
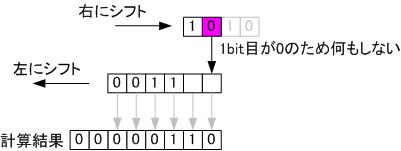▼ステップ 4
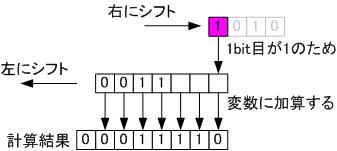右シフトが出来なくなったため計算終了です
▼プログラムを修正して掛け算を出来るように変更する
上記、掛け算の方法をそのままプログラムに反映させて作成してみます
#include <stdio.h>
//足し算
void add(unsigned short*a,unsigned short*b,unsigned short*c,int size){
c[0]=(a[0] & 0xFF)+(b[0] & 0xFF);
for(int i=1;i<size;i++){
c[i]=(a[i] & 0xFF)+(b[i] & 0xFF)+(c[i-1]>>8);
}
}
//引き算
void sub(unsigned short*a,unsigned short*b,unsigned short*c,int size){
c[0]=((~b[0]) & 0xFF)+0x01;
for(int i=1;i<size;i++){
c[i]=((~b[i]) & 0xFF)+(c[i-1]>>8);
}
add(a,c,c,size);
}
//配列のコピーもしくは in がNULLの場合クリア
void copy(unsigned short*in,unsigned short*out,int size){
if(in){
for(int i=0;i<size;i++){
out[i]=in[i];
}
}else{
for(int i=0;i<size;i++){
out[i]=0;
}
}
}
//左シフト
void left_shift(unsigned short*a,int size){
a[0]=a[0]<<1;
for(int i=1;i<size;i++){
a[i]=(a[i]<<1)|(a[i-1]>>8 & 0x01);
}
}
//右シフト
void right_shift(unsigned short*a,int size){
for(int i=0;i<size-1;i++){
a[i]=(a[i]>>1)|((a[i+1]<<7) & 0xFF);
}
a[size-1]=a[size-1]>>1;
}
//掛け算
void mul(unsigned short*a,unsigned short*b,unsigned short*c,int size){
for(int i=0;i<size*8;i++){
if(a[0] & 0x01){
add(b,c,c,size);
}
right_shift(a,size);
left_shift(b,size);
}
}
int main(){
unsigned short a[4],b[4],c[4];
//初期値の設定
a[3]=0x00;a[2]=0x00;a[1]=0x12;a[0]=0x34;
b[3]=0x00;b[2]=0x00;b[1]=0x56;b[0]=0x78;
//配列 c の初期化
copy(NULL,c,(sizeof(a)/sizeof(a[0])));
//掛け算の実行
mul(a,b,c,(sizeof(a)/sizeof(a[0])));
//表示
for(int i=(sizeof(a)/sizeof(a[0]))-1;i>=0;i--){
printf("%02x ",(unsigned char)(c[i] & 0xFF));
}
printf("\n");
return 0;
}
プログラムを実行
c:\>■■■.exe
06 26 00 60
上記プログラムは 0x00001234 * 0x00005678 を行っていますので
関数電卓で確認すると
0x1234 - 0x5678 = 0x6260060
電卓の計算結果と同一です
乗算方法が正しいことが確認できました
■割り算について考える
割り算の場合は、筆算で割り算の計算を行うのとまったく同じ仕組みで計算が行われます
▼次の割り算を行いたいと思います
▼ステップ 1
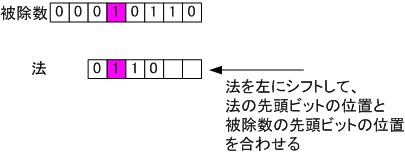▼ステップ 2
被除数から法が引けないため何もしません
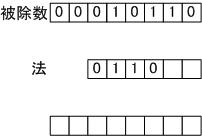▼ステップ 3
法を右シフトします
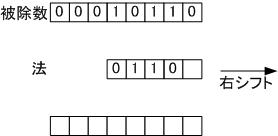▼ステップ 4
被除数から法を引くことが出来るため処理を行います
▼ステップ 5
法を右シフトします
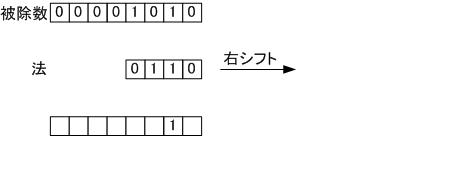▼ステップ 6
被除数から法を引くことが出来るため処理を行います
法が初期状態と同じシフト位置に来たため計算終了です
計算結果は 11 あまり 100 になります
▼プログラムを修正して割り算を出来るように変更する
上記、割り算の方法をそのままプログラムに反映させて作成してみます
#include <stdio.h>
//足し算 c=a+b
void add(unsigned short*a,unsigned short*b,unsigned short*c,int size){
c[0]=(a[0] & 0xFF)+(b[0] & 0xFF);
for(int i=1;i<size;i++){
c[i]=(a[i] & 0xFF)+(b[i] & 0xFF)+(c[i-1]>>8);
}
}
//引き算 c=a-b bufは計算処理に必要なバッファ
void sub(unsigned short*a,unsigned short*b,unsigned short*c,int size
,unsigned short*buf){
//2の補数をとる
buf[0]=((~b[0]) & 0xFF)+0x01;
for(int i=1;i<size;i++){
buf[i]=((~b[i]) & 0xFF)+(buf[i-1]>>8);
}
//足し算をする
add(a,buf,c,size);
}
//配列のコピーもしくは in がNULLの場合クリア
void copy(unsigned short*in,unsigned short*out,int size){
if(in){
for(int i=0;i<size;i++){
out[i]=in[i];
}
}else{
for(int i=0;i<size;i++){
out[i]=0;
}
}
}
//左シフト
void left_shift(unsigned short*a,int size){
a[0]=a[0]<<1;
for(int i=1;i<size;i++){
a[i]=(a[i]<<1)|(a[i-1]>>8 & 0x01);
}
}
//右シフト
void right_shift(unsigned short*a,int size){
for(int i=0;i<size-1;i++){
a[i]=(a[i]>>1)|((a[i+1]<<7) & 0xFF);
}
a[size-1]=a[size-1]>>1;
}
//掛け算 c=a*b a,b の値は計算により書き換えられます
void mul(unsigned short*a,unsigned short*b,unsigned short*c,int size){
for(int i=0;i<size*8;i++){
if(a[0] & 0x01){
add(b,c,c,size);
}
right_shift(a,size);
left_shift(b,size);
}
}
//比較 a<b と同等
int cmp(unsigned short*a,unsigned short*b,int size){
for(int i=size-1;i>=0;i--){
if((a[i]&0xFF)<(b[i]&0xFF)) return 1;
if((a[i]&0xFF)>(b[i]&0xFF)) return 0;
}
return 0;
}
//割り算 a:被除数 b:法 c:計算結果 a:余り size:配列のサイズ buf1,buf2:バッファ
//a の値は計算により書き換えられます
void div(unsigned short*a,unsigned short*b,unsigned short*c,int size
,unsigned short*buf1,unsigned short*buf2){
//配列を複製する
copy(b,buf1,size);
//法を左端に移動する
int shift=1;
for(int i=0;i<size*8;i++){
left_shift(buf1,size);
shift++;
if(buf1[size-1] & 0x80) break;
}
//被除数から法を引いてゆく処理と計算結果を作成する処理
while(shift--){
left_shift(c,size);
if(!cmp(a,buf1,size)){
sub(a,buf1,a,size,buf2);
c[0]=c[0] | 0x01;
}
right_shift(buf1,size);
}
}
int main(){
//変数
unsigned short a[4],b[4],c[4];
//計算に必要なバッファ
unsigned short buf1[4],buf2[4];
//初期値の設定
a[3]=0x12;a[2]=0x34;a[1]=0x56;a[0]=0x78;
b[3]=0x00;b[2]=0x00;b[1]=0x9A;b[0]=0xBC;
//配列 c の初期化
copy(NULL,c,(sizeof(a)/sizeof(a[0])));
//割り算の実行
div(a,b,c,(sizeof(a)/sizeof(a[0])),buf1,buf2);
//表示
for(int i=(sizeof(a)/sizeof(a[0]))-1;i>=0;i--){
printf("%02x ",(unsigned char)(c[i] & 0xFF));
}
printf("\n");
for(i=(sizeof(a)/sizeof(a[0]))-1;i>=0;i--){
printf("%02x ",(unsigned char)(a[i] & 0xFF));
}
printf("\n");
return 0;
}
プログラムを実行
c:\>■■■.exe
00 00 1e 1e
00 00 2c 70
上記プログラムは 0x12345678 / 0x00009ABC を行っていますので
関数電卓で確認すると
0x12345678 / 0x9ABC = 0x1E1E あまり 0x2C70
電卓の計算結果と同一です
除算方法が正しいことが確認できました
■まとめ
short型配列の一つの要素に対して1バイトの値を表現できるようになっていますので
配列の要素を増やせば、メモリが有る限りいくらでも計算桁数を増やすことが出来るはずです
このプログラムだと内部の値の持ち方が2進のため、いざ何か応用しようと考えると、
10進から16進に変換したり、戻したりするのが厄介ですから、
直接10進数で計算する方式で作成した方が流用が利くかもしれません。
20060924 作成
▲トップページ
>
プログラミングの実験